
オプション取引入門講座 第10回 2項モデル(バイノミナルモデル)
講師:有馬秀次
1.2項モデル(バイノミナルモデル)の意味と計算
≪2項モデルとは何か≫
2項モデル(バイノミナルモデル)は、ツリー(樹形)型の価格変動モデルを利用してオプション価格(プレミアム)を計算する近似計算法です。発案者3人の名前から呼び名がついたCRRモデル(コックス・ロス・ルービンシュタイン)も、2項モデルとして広く知られています。
2項モデルは、原資産価格やオプション価格の変動パターンを樹形に当てはめてみることでオプション価格を見つけだそうとするモデルです。オプション価格は原資産価格の動きに付随しているので、将来の原資産価格がわかれば、そこから逆算して現在のオプション価格が求められるというものです。
◆B&Sモデルとの違い
2項モデルでは、B&Sモデルのような高度な数学的テクニックを使わずに計算が行えます。計算に時間がかかるのが難点ですが、B&Sモデルと違ってアメリカンタイプやエキゾチック(非定型オプション)のプレミアム計算ができる点が長所で、オプション評価法の定番になっています。

2項モデルの計算には、汎用ブラックショールズ式と同様に、行使価格、期間、原資産価格、原資産利回り、短期金利(安全利子率)、ボラティリティ(予想変動率)の6つの情報が必要です。
◆ツリー(樹形)型とは
ツリー(樹形)型とは、木が枝分かれしていく様子をいいます。2項樹形は、2つに枝分かれを繰り返していくもので、枝分かれしたもの同士が再結合するという構造の樹形です。ちょうど、ひし形の格子を連ねた形をしているので、これを格子モデルとして説明していきます。
2項モデルでは、原資産価格が格子上を上昇するのか下降するのか、という単純な動きを繰り返すと仮定することによって、原資産価格の変動が説明できると考えています。

≪ノード(結節点)≫
2項モデルで原資産価格が枝分かれしていく経路が再結合する節点のことをノード(結節点)といいます。ノード(結節点)は、価格が上がるか下がるかの分岐点を示します。
3つのノードが形成する三角形を格子の最小単位として1格子と呼ぶことにします。また、1格子を期間の最小単位として1期間と呼ぶことにします。隣り合う格子は、互いにノードを共有しています。

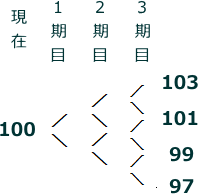
例えば、現在の原資産価格が100円である場合、1期間後に101円に上昇するか、99円に下降するかのどちらか1つの動きをするとします。
1期間後に101円に上昇すると、2期目はさらに上昇して102円になるか、下降して100円になるかです。
1期間後に99円に下降すると、2期目は上昇して100円になるか、さらに下降して98円になるかです。
1期目で上昇して2期目で下降した場合と、1期目で下降して2期目で上昇した場合の原資産価格は、共に100円となります。

格子を3期間に拡張すると、3期間後には、4通りの原資産価格が予想されます。
1期目は、ノード100円から101円に上がるか99円に下がるか、という2通りの経路しかありません。格子数は1つです。
2期目は、ノード101円から102円に上がるか100円に下がるかという経路と、ノード99円から100円に上がるか98円に下がるかという経路に広がります。格子数は2つになります。
ノード101円から下降した場合と、ノード99円から上昇した場合は共に同じノード100円に到達します。
3期目には、3つの格子ができることになります。
このように、n期間後にはn個の格子ができることがわかります。
3期間の全体の格子数は、6個(1+2+3=6)になります。
n期間の全体の格子数は、n(n+1)/2 個と計算されます。
n期間後の格子数はn個
ノード数は n+1
全体の格子数は n(n+1)÷2
◆オプション価値とオプション価格
オプション価格とは、市場でオプション価値に付けられる値段のことです。したがって、オプション計算モデル(BSモデル、2項モデル)で計算しているオプション価値というのは理論価格のことを意味します。
2.2項モデルの計算
2項モデルは、(1)原資産価格を予測する、(2)予測された将来のオプション価格から、現在のオプション価格を逆算する、という計算を行うために格子パターンを利用しています。
(1)原資産価格の予測
現在の原資産価格から将来の原資産価格を予測します。
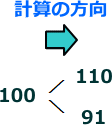
例えば、現在の原資産価格が100円であるとして、1期間後に10%上昇するか下降するかの仮定をすると、1期間後の原資産価格は、
110円(100×1.1=110)か、91円(100÷1.1=90.9)と予測されます。
上昇率(Up)をU=1.1、下降率(down)をd=1÷U=0.91 とすると、
100×U または 100×d
で、一期先の原資産価格の計算が行えます。
CRRモデルでは、U=e σ√t 、d=e -σ√t と設定して計算します。
※実際の計算では、1期間の上昇または下降はごく微小な数値ですが、ここでは計算をわかりやすくするために、10%という大きな数値で説明しています。
(2)オプション価値の計算
◆現在のオプション価値の計算
将来の原資産価格が予想されると、現在のオプション価値が計算できます。
例えば、行使価格100円のコールオプションの場合、オプション価値は、
原資産価格が110円に上昇した場合のオプション価格(Cu)は、10円(110-100=10)
原資産価格が91円に下降した場合のオプション価格(Cd)は、0円(オプション放棄) と計算されます。

C=コールオプション価格、S=原資産価格、K=行使価格
※uは上昇(up)、dは下降(down)を意味しています。
◆1期前のオプション価値の計算(後戻し計算)
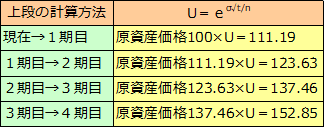
2項モデルのオプション計算式を使うと、1期間後の2つのオプション価格を使って、1期前のオプション価格を計算することができます。

例えば、Cu=10、Cd=0 P=0.6 R=1 であった場合、次のように計算されます。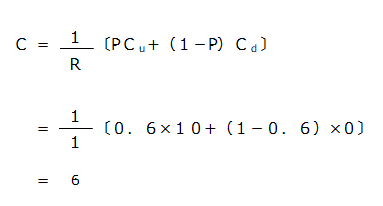
C=コールオプション価格、R=現在価値を計算する割引率、P=確率
P=(R-d)/(u-d)
ただし、u=e σ√t/n d=1/u R=e r ・t/n
e=ネピアの数(すう)、σ=予想変動率、r=短期金利、t =オプション行使期間、n=分割数
≪2項モデルのオプション計算式≫
1格子期間の原資産の動きと安全資産の動きを無裁定価格評価理論を使って組み合わせると、オプションのキャッシュフローが模倣できます。
2項モデルのオプション計算式は、この関係を連立方程式にして解いて求めたものです。
ここでいう原資産とは、オプション取引の対象商品で、株式オプションであれば株式のことを、ドル/円の通貨オプションであればドルのことを意味します。
安全資産というのは、デフォルトリスク(債務不履行)のない資産のことで、国債のような商品を意味します。利率が確定している大手銀行の定期預金をイメージしてもよいでしょう。数式上では、短期の借入金はマイナスの安全資産(─B)として扱います。
株式オプションを例にとり、原資産である株式とマイナスの安全資産である借入金で、オプションと同じキャッシュフローを模倣してみましょう。
数式 C=ΔS─B とおき、これを使ってオプションが上昇した場合(Cu)と下降した場合(Cd)の連立方程式を設定します。R=(1+r)で r は安全利子率を意味します。r が1%であるとき、Rは1.01となります。
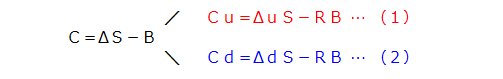
Δ(デルタ):ヘッジ比率、S:原資産価格、C:コールオプション価格、B:借入金(負の安全資産)
この連立方程式をΔ(デルタ)とBについて解くと、
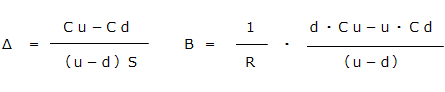
C=ΔS-B だから、
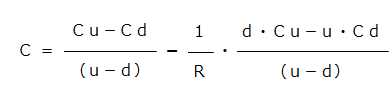
ただし、U=e σ√t/n d=1/U R=e r ・t/n
※ここで、R=er・t/n は、現在価値を計算する割引率を示しています。
さらに、P=(R-d)/(u-d)とおくと、この計算式は、下記のように変形できます。
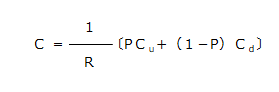
P=確率、n=期間数、 r=短期金利、t =期間、q=原資産利回り、e=ネピアの数(すう)
この式は、オプションの期待値(平均値)を求め、そこから現在価値を計算することを意味しています。
ここで、原資産が利回り q %をもつ場合には、r %を(r-q)%に入れ替えて、Pを計算します。
P=〔e(r-q)t-d)/(u-d)〕
q は、原資産が株式の場合は配当利回り、原資産が外国為替の場合は外国通貨の金利を意味します。
参考 : 連立方程式の計算
≪2項モデル計算の実際≫
2項モデルでは、格子数が多いほど計算は正確になります。しかし、計算時間も長くなるため、通常35期間ぐらいで計算しています。35期間でも、630回(35×36÷2=630)もの繰り返し計算が必要になります。
オプション価格は、次の3つのステップで計算されます。
(1)原資産がどのように変動するか、各格子点順に満期日まで原資産価格を計算します。
(2)満期日のオプションの行使価値(本源価値)を計算します。
(3)2項モデル式を使って、満期日のオプション価値から1期間ずつ、格子を現在までさかのぼる後戻し計算をします。
◆ヨーロピアンタイプのオプション計算
ヨーロピアンコールオプション
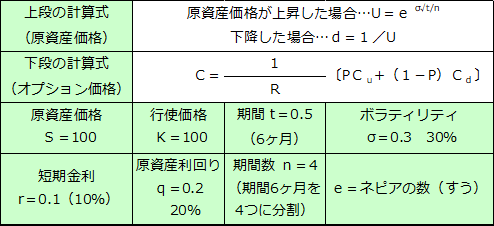
コールオプション価格 : 5.25
表の上段…原資産価格 下段…オプション価格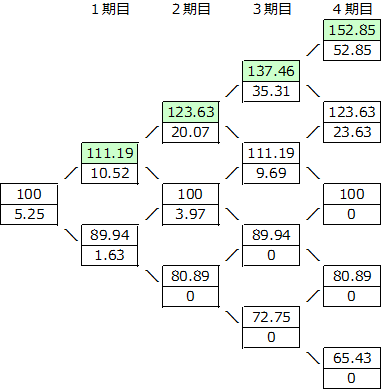
※下段のオプション価格は、1~3期目はオプションを保有しているときのオプション価値、4期目はオプションを行使したときのオプション価格となります。
≪解説≫
原資産価格が上昇し続けた場合を例にとって計算してみましょう。
オプション価格をさかのぼる後戻し計算をしてみましょう。

◆アメリカンタイプのオプション計算
2項モデルでは、アメリカンタイプ(満期日前にいつでも行使できる)のプレミアム計算が行えます。オプションが満期日前に行使されるのは、満期日まで保有するより有利な場合です。2項モデルでは、オプションを早期に行使した方が有利かどうか、各ノ-ド(格子点)で調べることができます。
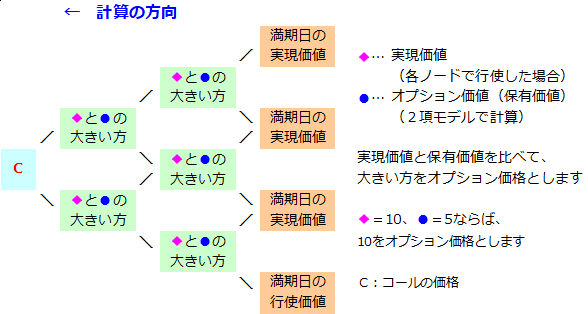
アメリカンタイプの計算は、各ノードで行使した場合の実現価値と、2項モデルで一期先の期待値から計算したオプション価値(保有価値)を比べて、大きい方をその時点のオプション価値として、格子をさかのぼっていく方法です。
※実現価値とは、オプションを早期に行使した場合のオプション価値のことです。これを行使価値と呼ぶと行使価格と混同しやすいので、実現価値と言い換えさせていただきました。
アメリカンコールオプション

コールオプション価格 : 6.14
表の上段…原資産価格 中段… 実現価値 下段…保有価値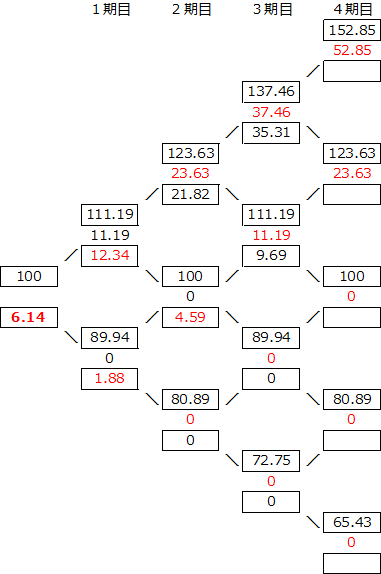
※中段の実現価値は、オプションを行使した場合のオプション価値で、上段の原資産価格から行使価格100円を差し引いた値です。原資産価格が100円以下の場合にはオプションは行使されませんので、実現価値は0円となります。
※下段の保有価値は、オプションを保有しているときのオプション価値です。4期目は満期のため、保有価値は空欄となっています。
≪解説≫
原資産価格が上昇し続けた場合を例にとって計算してみましょう。

オプション価格をさかのぼる後戻し計算をしてみましょう。
中段の実現価値と下段の保有価値を比べて、大きい方をオプション価格とします。
計算期間の分割の仕方によって近似値にブレが発生しますが、最小計算期間を短くする(分割数を大きくする)ことでB&Sモデルの値に近づいていきます。

この計算法は、株価指数、外国為替、先物を原資産とするオプションに利用されています。
3.個別株式オプションのアメリカンタイプの計算
オプションの原資産は、(1)原資産の利回りが連続的に発生するタイプ、(2)原資産の利回りがある時点にまとめて支払われるタイプ、の2つに分けられます。
◆原資産の利回りが連続的に発生するタイプ
原資産の利回りが連続的に発生するタイプは、株価指数、外国為替、先物などを原資産とするオプションです。株価指数、外国為替、先物などのオプション計算は、先に説明した手順で計算します。
◆原資産の利回りがある時点にまとめて支払われるタイプ
原資産の利回りがある時点にまとめて支払われるタイプは、個別株式や利付債を原資産とするオプションです。配当支払いのある株式オプションでは格子のノードが再結合しなくなるという問題点が発生するため、格子モデルに修正を加えたものを使って評価を行います。
≪配当支払いのある株式オプションの問題点≫
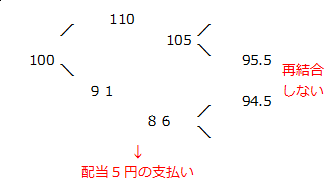
配当が支払われると、格子のノードが再結合しなくなります。
例えば、配当5円が1期後に支払われた場合、2期目のノードは一致しなくなります。配当支払後の原資産価格は、配当分だけ下がると考えられるからです。
配当支払後のノードは原資産価格が右例のように下がり、結果的に次期のノードは再結合しなくなります。
こうしたツリー(樹形)型では、計算が複雑になってしまうという問題があります。
この問題を解決する便法として考えられた方法が、予定配当金額を原資産から切り離して2項モデルを適用するという方法です。
株価(S)=実質株価(S') + 配当の現在価値(D0)
この方法は、配当支払いが予定されている場合、その支払いが起こると、株価(原資産価格)から配当分だけ価格が下がることがわかっているので、この配当分を株価から差し引いた価格が確率的な価格変動過程に従うと仮定するものです。
現在の株価から支払予定配当額の現在価値を差し引いたものを実質株価(S’)と呼ぶことにします。
配当(D)を短期金利(安全利子率)で割り引くと、配当の現在価値(D0)が計算されます。
D0=D×e-rt S'=S - D0
実質株価S'は、上昇(U)するか下降(D)するかの2項過程に従うことになります。
現在の株価がSであるとき、配当の現在価値D0を求めて実質株価S'を計算します。この実質株価S'を原資産として2項モデルの計算を行います。
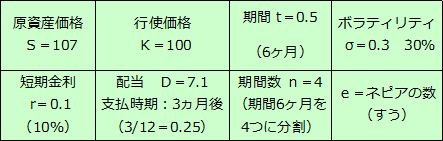
3ヵ月後に配当支払いを予定されている株式オプション(期間 6ヶ月)のコール価格を求めてみましょう。
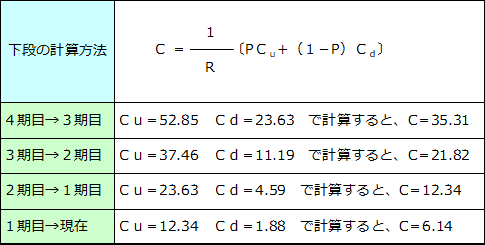
コールオプション価格 : 12.02
表の上段…原資産価格 中段… 実現価値 下段…保有価値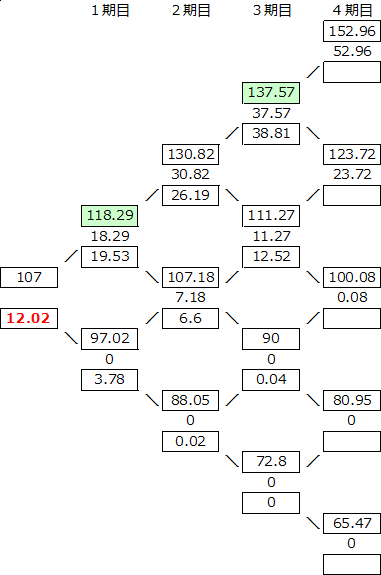
現在の株価(S)が107であるとき、配当(D)=7.1から、配当の現在価値(D0)=6.92と計算されます。
したがって、S'=S-D0=100.08となります。
1期目の株価上昇=S'×(eσ√t)+D0×ert
=100×(e0.3√0.125)+6.92×e0.1×0.125
=118.29
3期目の株価上昇3回=S'×(eσ√t)3
=100×(e0.3√0.125)3
=137.57
4.B&Sモデルと2項モデルの違い
B&Sモデルと2項モデルの違いは、原資産の価格付けを連続的なものと考えるか、離散的なものと考えるかにあります。「連続」か「離散」かという概念は、物の量を液体で量るのか固体(粒子の数)で量るのか、という例えに類似しています。
B&Sモデルでは、原資産の値動きを切れ目のない液体のようなものとして捉えて、「連続的変動」と仮定しています。その結果、オプションの複製を、微分方程式(瞬間の関係式)として解いたものです。
2項モデルでは、原資産の値動きを断続的に発生するものとして捉えて、「離散的変動」と仮定しています。その結果、オプションの複製を、連立方程式(短期間の関係式)として解いたものです。

2項モデルで、格子の計算期間を無限に短くしていくと、連続的な変動として捉えることになります。したがって、計算する格子数を無限に増やせば、2項モデルの答えは、B&Sモデルの値と一致することになります。
5.アメリカンタイプのオプション価格計算の裏技
ヨーロピアンタイプのオプション価格は、BSモデルを利用して短時間で計算できます。しかし、アメリカンタイプのオプション価格は、BSモデルに相当するモデルがなかったため、2項モデルを利用して計算していました。
2項モデルでは、計算期間(格子数)を大きくするほど、誤差の小さい答えを得ることができます。2項モデルで精度のよい計算をするには、計算期間(格子数)を無限に増やしていけばよいのです。
しかし、計算期間(格子数)を増やすと、計算に要する時間も長くなってしまいます。どうしたら少ない計算期間(格子数)で、誤差の小さい答えを得られるか…これは、2項モデルの最大の関心事です。
そこで、アメリカンタイプの計算に、ヨーロピアンタイプの計算を利用する方法が考案されました。
ヨーロピアンタイプのオプション価格を、計算期間(格子数)を10回ぐらいに設定して計算したものと、BSモデルで計算した答えとの間には大きな誤差が生じます。しかし、計算期間(格子数)を1万回ぐらいに設定して計算すると、BSモデルの計算結果と一致します。
ヨーロピアンタイプのオプション価格では、
2項モデルで計算期間(格子数)を無限に大きくした計算結果と、BSモデルの計算結果が一致する。
2項モデル(計算期間:無限に大きい)=BSモデル
しかし、計算期間(格子数)を1万回に設定して計算するのは、時間がかかりすぎて大変です。
そこで、ヨーロピアンタイプの計算における誤差(少ない格子数(例えば4回)で計算した答えと、BSモデルの答えとの誤差)が、アメリカンタイプの計算にも同様にあると仮定する方法が考えられました。
すると、計算期間(格子数)4回で計算したアメリカンタイプの計算の答えに、ヨーロピアンタイプの計算の誤差を加えることで、計算期間(格子数)1万回で計算した答えに近似する答えを得ることができます。
なお、計算期間(格子数)4回で計算したアメリカンタイプとヨーロピアンタイプの計算の差をBSモデルの答えに加算して計算する方法…と考えても、計算結果は同じです。
≪4期間の場合≫

アメリカン(4期間)+ヨーロピアン(BS)-ヨーロピアン(4期間)=6.14+5.74-5.25≒6.63
≪参考:オプションでよく目にする文字記号≫
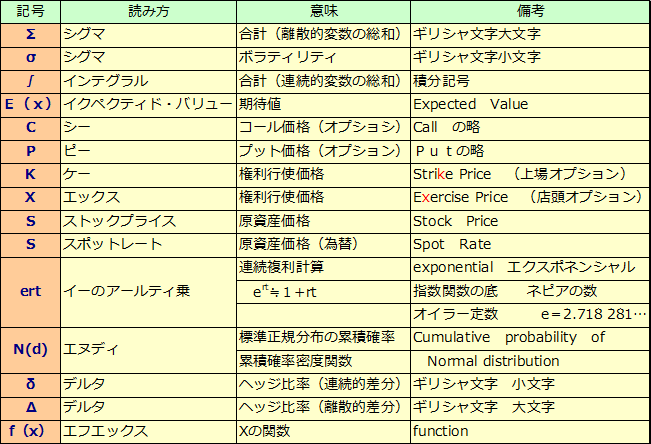
まとめ
2項モデルとは何か
ツリー(樹形)型の価格変動モデルを利用してオプション価格を計算する近似計算法
ノード(結節点)…原資産価格が枝分かれしていく経路が再結合する節点
2項モデルの計算
(1)原資産価格の予測…現在の原資産価格から将来の原資産価格を予測する
(2)オプション価値の計算…現在のオプション価値の計算
1期前のオプション価値の計算(後戻し計算)
オプション価格の計算ステップ
(1)各格子点順に満期日まで原資産価格を計算する
(2)満期日のオプションの行使価値(本源価値)を計算する
(3)2項モデル式を使って、満期日のオプション価値から1期間ずつ後戻し計算する
配当支払いのある株式オプション
配当が支払われると、格子のノードが再結合しなくなるという問題点が発生する
格子モデルに修正を加えたものを使って評価する
B&Sモデルと2項モデル
2項モデルで計算する格子数を無限に増やせば、B&Sモデルの値と一致する
アメリカンタイプのオプション価格計算の裏技…少ない計算期間数で計算したアメリカンタイプのオプション価格に、ヨーロピアンタイプの計算で発生する誤差を加えることによって、よりよい近似値が得られる
問題と解答
- 2項モデル(●●ノミナルモデル)は、ツリー(樹形)型の価格変動モデルを利用してオプション価格(プレミアム)を計算する近似計算法です。発案者3人の名前から呼び名がついた●●Rモデル(コックス・ロス・ルービンシュタイン)も、2項モデルとして広く知られています。
- 2項モデルで原資産価格が枝分かれしていく経路が再●●する節点のことをノード(結節点)といいます。●●●(結節点)は、価格が上がるか下がるかの分岐点を示します。隣り合う格子は、互いにノードを共有しています。
- 2項モデルは、(1)●●●価格の予測、(2)予測された将来のオプション価格から、●●のオプション価格を逆算する、という計算を行うために格子パターンを利用しています。2項モデルのオプション計算式を使うと、1期間後の2つのオプション価格を使って、1期前のオプション価格を計算することができます。
- 1格子期間の原資産の動きと●●資産の動きを無裁定価格評価理論を使って組み合わせると、オプションのキャッシュフローが模倣できます。2項モデルのオプション計算式は、この関係を●●方程式にして解いて求めたものです。
- オプション価格は、(1)各格子点順に満期日まで●●●価格を計算する、(2)満期日のオプションの行使価値(本源価値)を計算する、(3)2項モデル式を使って、満期日のオプション価値から1期間ずつ●●し計算をする、という3つのステップで計算されます。
- 2項モデルでは、●●●カンタイプのプレミアム計算が行えます。アメリカンタイプの計算は、各ノードで行使した場合の実現価値と、2項モデルで一期先の期待値から計算したオプション価値(保有価値)を比べて、●●●方をその時点のオプション価値として、格子をさかのぼっていく方法です。
- 配当支払いのある●●オプションでは、格子の●●●が再結合しなくなるという問題点が発生します。配当支払後の原資産価格は、配当分だけ下がると考えられるからです。そのため、予定配当金額を原資産から切り離して2項モデルを適用します。
- B&Sモデルでは、原資産の値動きを連続的変動と仮定した結果、オプションの複製を、●●方程式(瞬間の関係式)として解いたものです。2項モデルでは、原資産の値動きを離散的変動と仮定した結果、オプションの複製を、●●方程式(短期間の関係式)として解いたものです。
- 2項モデルで、格子の計算期間を無限に短くしていくと、●●的な変動として捉えることになります。したがって、●●●ピアンタイプのオプション価格では、2項モデルで計算期間を無限に大きくした計算結果と、ブラック・ショールズ式の計算結果は一致します。
- 少ない計算期間数で得た●●●カンタイプのオプション価格に、同じヨーロピアンタイプの計算で発生する誤差を加えることによって、より精度の高いアメリカンタイプの●●値を得ることができます。
(答え)バイ、CR
(答え)結合、ノード
(答え)原資産、現在
(答え)安全、連立
(答え)原資産、後戻
(答え)アメリ、大きい
(答え)株式、ノード
(答え)微分、連立
(答え)連続、ヨーロ
(答え)アメリ、近似
